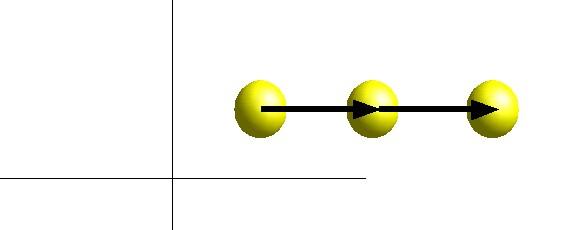
Object motion is represented with vectors.
Velocity is a vector:
Vector direction is direction of movement
Vector magnitude is speed of movement
Velocity vector corresponds to amount object will move in one unit of time.

Displacement = Velocity * time
If an object starts at position P0,
with velocity V,
after t time units, its position P(t) is:
P(t) = P0 + V * t
Note: choice of units is arbitrary, as long as things are consistent.
e.g. use meters for distance, seconds for time, and meters/second for velocity.
Don't try to combine meters/second with miles/hour, for instance.
The previous formula only works if the object moves with a constant velocity.
In many cases, objects' velocities change over time.
In such a case, velocity is a function that we integrate.
Displacement = 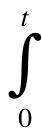 Velocity dt
Velocity dt
In complex motion, there isn't an analytical solution (i.e. a simple formula).
Euler integration approximates an integral by step-wise addition.
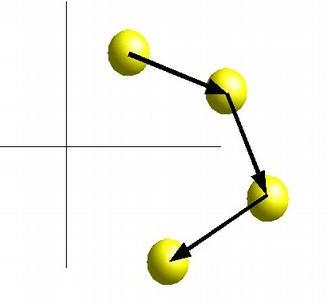
At each time step, we move the object in a straight line using the current velocity:
dt = t1 - t0
P(t1) = P(t0) + V * dt
Velocity is the integral of acceleration:
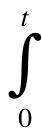 Acceleration dt
Acceleration dt
Applying Euler integration again gives:
dt = t1 - t0
Acc = computeAcceleration()
Vel = Vel + Acc * dt
Pos = Pos + Vel * dt
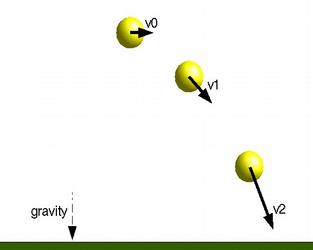
Gravity near the Earth's surface produces a constant acceleration of 9.8 m/sec2
In this case:
Acc = Vector([0, -9.8, 0])
Example: gravbounce.py
Newton's 2nd Law of Motion:
Which can be rewritten as
If an object has mass M, and force F is applied to it,
its motion can be calculated via Euler integration:
Acc = F / M
Vel += Acc * dt
Pos += Vel * dt
Note that F, Acc, Vel, and Pos are all vectors. M is a scalar.
F = (G * M1 * M2) / d2
For a complete simulation, we need to calculate the force on each object every frame.
When multiple forces are applied, their vectors are added.
Example: gravorbit.py
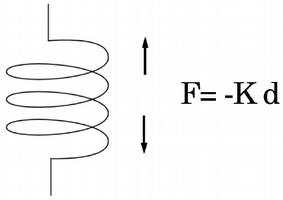
Drag (slow moving objects):
F = Cdrag * V
Drag (fast moving objects):
F = Cdrag * V2
Buoyancy:
F = ρliquid * g * Volume
Example: buoyancy.py
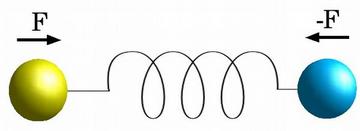
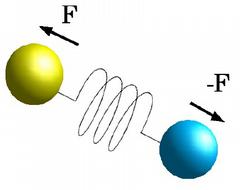
Spring is modeled as 2 point masses, linked by the spring
Equal but opposite force is applied to each end
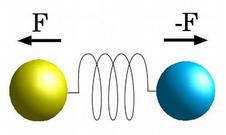
Vector between the points is used to compute displacement and the direction of force:
v = point1 - point0
displacement = v.length() - restLength
v.normalize()
force = springConstant * displacement * v
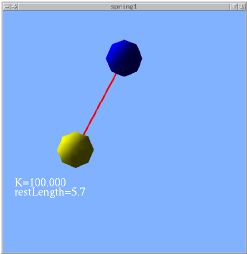
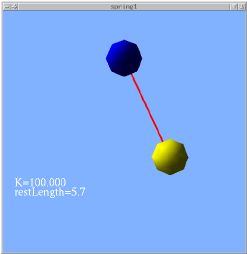
Two classes needed: PointMass and Spring
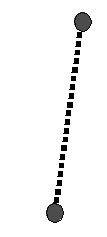
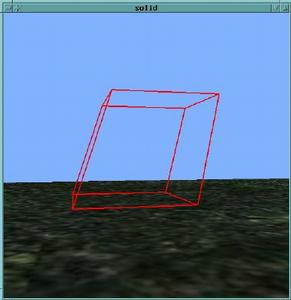
Solid objects can be simulated as a collection of springs
Stiff springs (large spring constant) produce rigid objects.
Loose springs produce jello-like objects.
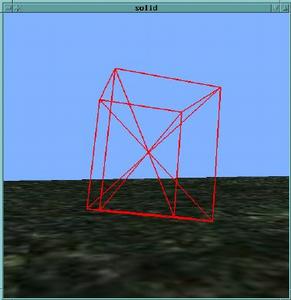
Often, additional internal springs are needed to keep a shape from collapsing
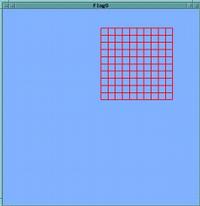
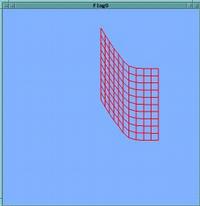
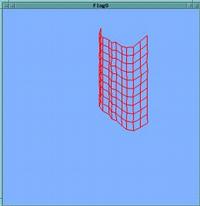
Cloth can be simulated by a mesh of springs
| 
| 
|
Diagonal springs are again useful, to keep the mesh from collapsing easily
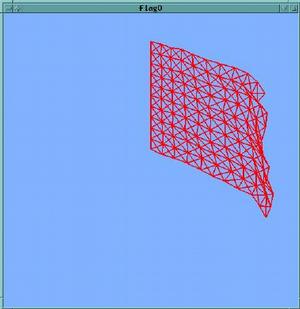
Spring calculations are prone to "numerical explosion"

| 
| 
|
| Possible solutions: |
|
