Randomness is useful for improving the 'quality' of applications in many different ways.
We often would like the behavior of a program to change or be unpredictable - to not be exactly the same every time we run it.
In other cases, randomness helps eliminate unwanted artifacts, such as obvious, excessively regular or repeated patterns. These include patterns in the appearance and in the movement of objects.
 | 
|
Things that can be randomized include:
Randomness is added to programs by using random numbers. These are generated by random number functions.
Python has a package called random.
Two of the functions it provides are:
Returns a random floating point number between 0 and 1.
Returns a random floating point number between a and b.
Most computers cannot generate truly random numbers.
The functions random() and uniform() are actually pseudo-random number generators.
This means that they use complex mathematical functions whose values, when viewed in a sequence, look fairly random. They won't pass advanced statistical tests for real randomness, but they're close enough for most work.
However, because they're mathematical functions, they're predictable.
Every time a program is started from scratch,
these functions will return the exact same sequence of numbers,
which can mean that your supposedly random program behaves
exactly the same way each time it's run.
This can be avoided by using the random package's seed function, which gives the function a different starting point to use, instead of the default.
random.seed(n)
In order
to get a different sequence of random numbers each time you run
your program, this seed-value must always be different.
A quick & easy way to do this is to use the current time:
import random, time
random.seed(time.time())
In some cases, you might want to be able to exactly reproduce a particularly interesting run of your program. Using the same seed-value will result in the same sequence of random numbers, so if you print out & record the seed number used whenever your program starts, you can plug that particular seed in again later to reproduce the run.
Using the current time is an alternative way to get one random number, since the exact time that a program will be run is generally random. But, this cannot be used more than once in a program, because once the program starts, the time values returned will form a fairly predictable sequence.
Random numbers can come in different distributions.
This refers to how frequently the various numbers are returned by your random function.
The basic functions (random() & uniform())
return uniform distributions - in other words, each possible number is equally
likely to be returned.
If you call the function a large number of times, then you
can expect each possible number to be returned about (but not exactly)
the same number of times.
This is equivalent to the fact that if you flip a coin 1,000,000 times,
you would expect to get roughly, but not exactly, 500,000 heads and 500,000 tails.
The following plot comes from calling int(random() * 100) 100,000 times. It shows how many times each of the possible values (from 0 to 99) was returned.
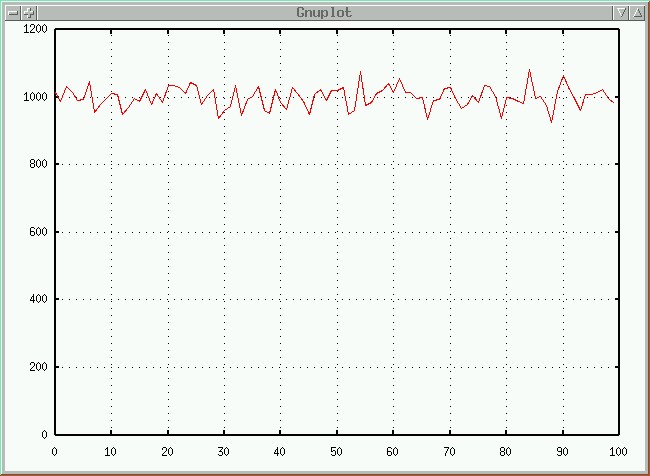
As expected, each number is returned roughly 1,000 times, with a moderate amount of variation, but no tendency to favor one number or any other real pattern.
Sometimes we would like a different distribution.
Another common distribution is the bell curve (or gaussian distribution). In this distribution, one small range of numbers is returned more frequently than others, with values further from the center of the distribution returned less and less frequently.
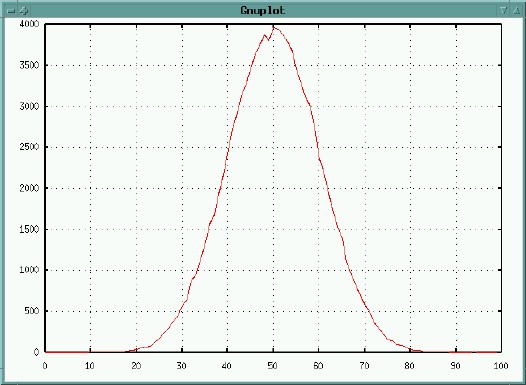
The function random.gauss(center, deviation) returns random numbers in a gaussian distribution.
The first argument (center) is the central number that the return
values will be clustered around. The second argument (deviation)
is the standard deviation of the distribution - this measures how broad the
bell curve is; roughly 2/3 of all returned values will be within +/- deviation
of the center value.
Example: a gaussian distribution lets you place objects randomly, but clustered about a center.
| Uniform | Gaussian |
|---|---|

| 
|
Choosing a random point in 2D or 3D space is simple - just pick a random X, Y, and Z.
Choosing a random point on the surface of a sphere is a bit trickier.
Some reasons for wanting to get a random point on a sphere:
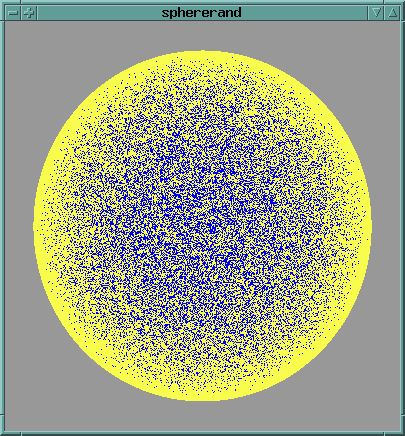
One obvious way to pick a random point is to just get a random X/Y/Z point, and then normalize it - this will force the point to be on the surface of the unit sphere.
Vector3 point;
point[0] = drand48() * 2.0 - 1.0;
point[1] = drand48() * 2.0 - 1.0;
point[2] = drand48() * 2.0 - 1.0;
point.normalize();
However, the points will not be distributed uniformly. The non-normalized points will uniformly fill a cube; a slightly above-average number of points from the corners of the cube will be normalized to certain areas of the sphere.
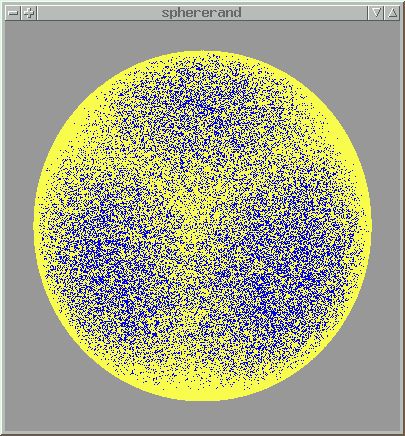
A better way to pick points is based on map projections.
The simplest map projection to use is a latitude-longitude (or Plate-Carree) projection. In this case, we choose a random latitude & longitude on the sphere's surface, and then convert that into the corresponding X/Y/Z values.
Vector3 point;
float lat, lon;
lat = drand48() * M_PI - M_PI_2;
lon = drand48() * M_PI * 2.0;
point[0] = sin(lon) * cos(lat);
point[1] = sin(lat);
point[2] = cos(lon) * cos(lat);
However, this will produce a higher concentration of points near the poles.
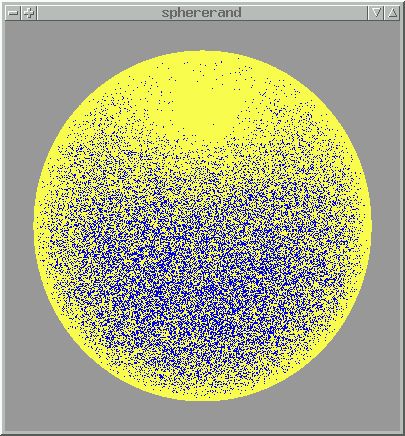
In some cases this sort of distribution may be desired, so this technique is worth remembering.
To get a uniform distribution of points across the sphere, we need to use an equal-area projection. A cylindrical projection - choosing a random Y value in combination with a random longitude - will give us this result.
longitude = random.uniform(0, 2*pi)
y = random.uniform(-1, 1)
point = Vector([sin(longitude) * cos(asin(y)), y, cos(longitude)*cos(asin(y))])