Choosing a random point in 2D or 3D space is simple - just pick a random X, Y, and Z.
Choosing a random point on the surface of a sphere is a bit trickier.
Some reasons for wanting to get a random point on a sphere:
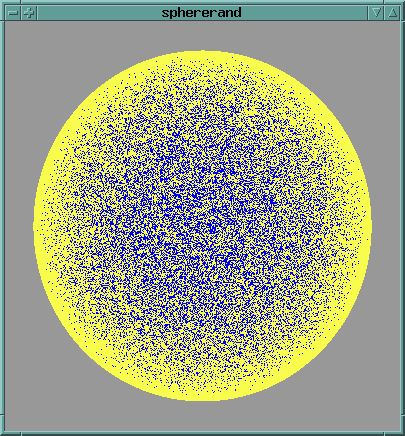
One obvious way to pick a random point is to just get a random X/Y/Z point, and then normalize it - this will force the point to be on the surface of the unit sphere.
Vector3 point;
point[0] = drand48() * 2.0 - 1.0;
point[1] = drand48() * 2.0 - 1.0;
point[2] = drand48() * 2.0 - 1.0;
point.normalize();
However, the points will not be distributed uniformly. The non-normalized points will uniformly fill a cube; a slightly above-average number of points from the corners of the cube will be normalized to certain areas of the sphere.

A better way to pick points is based on map projections.
The simplest map projection to use is a latitude-longitude (or Plate-Carree) projection. In this case, we choose a random latitude & longitude on the sphere's surface, and then convert that into the corresponding X/Y/Z values.
Vector3 point;
float lat, lon;
lat = drand48() * M_PI - M_PI_2;
lon = drand48() * M_PI * 2.0;
point[0] = sin(lon) * cos(lat);
point[1] = sin(lat);
point[2] = cos(lon) * cos(lat);
However, this will produce a higher concentration of points near the poles.
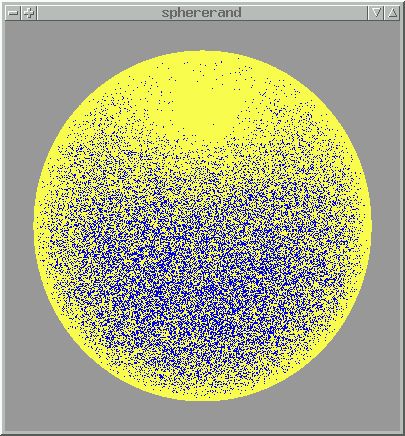
In some cases this sort of distribution may be desired, so this technique is worth remembering.
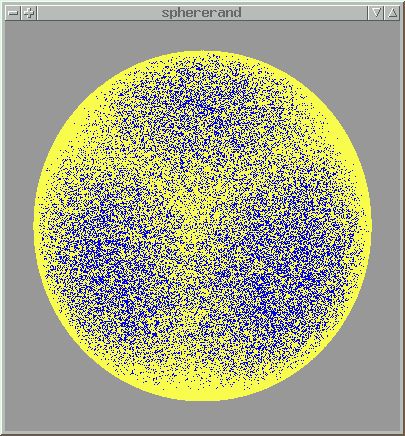
To get a uniform distribution of points across the sphere, we need to use an equal-area projection. A cylindrical projection - choosing a random Y value in combination with a random longitude - will give us this result.
longitude = random.uniform(0, 2*pi)
y = random.uniform(-1, 1)
point = Vector([sin(longitude) * cos(asin(y)), y, cos(longitude)*cos(asin(y))])