Vectors

A vector is a direction and magnitude (length). Vectors are used to represent many different things - light source directions, surface orientations, relative distances between objects, etc.

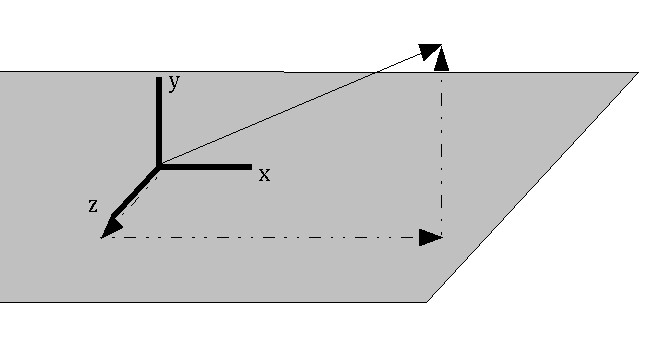
We normally describe a vector as a triplet of (X, Y, Z) values - (v_x, v_y, v_z) represents a vector that points v_x units in the direction of the X axis, v_y units in the direction of the Y axis, and v_z units in the direction of the Z axis.

e.g., (2, 0, 0) is a vector pointing in the direction of the X axis, 2 units long. (1, 1, 0) is a vector pointing at a 45 degree angle between the X and Y axes, 1.414 units long.

The magnitude of a vector (x,y,z) is its "Euclidean" length - the square root of x² + y² + z².

Operations

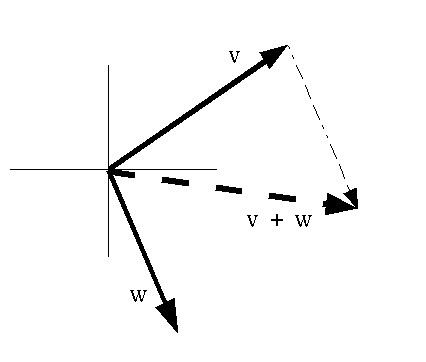
Two vectors can be combined by adding their corresponding components together.
i.e. (v_x, v_y, v_z) + (w_x, w_y, w_z) is (v_x+w_x, v_y+w_y, v_z+w_z).
Or, written more expansively:

  | vx |     | wx |     | vx + wx |
  | vy |  +  | wy |  =  | vy + wy |
  | vz |     | wz |     | vz + wz |

The result is a vector that is equivalent to sticking the vector W onto the end of vector V, and creating a new vector from the beginning of V to the end of W.

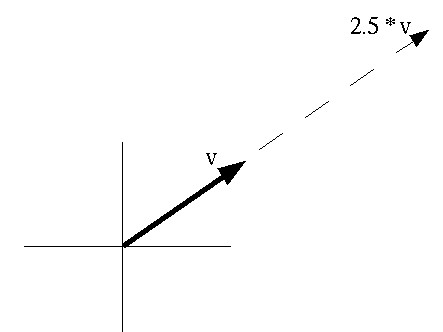
A vector can be multiplied by a single number (a "scalar") to change its length without changing its direction.

        | vx |  =  | s * vx |
  s  *  | vy |  =  | s * vy |
        | vz |  =  | s * vz |

next