Fractals feature fine detail at arbitrary scales.
They are usually highly irregular.
They exhibit some degree of self-similarity.
They can be mathematically defined.

Classic fractal image, described by Benoit Mandelbrot.
The set is those points (c) in the complex plane for which the formula:
z = z2 + c
remains finite when applied iteratively.
This can be estimated by
z = c
for i in range(0, maxIterations):
z = z*z + c
if abs(z) > 2: return False
return True
Sample code: glmandelbrot.py




Fractal terrain can be generated in different ways, some using statistical filtering of noise.
Another, simple method is "midpoint subdivision".
Start with a basic terrain model, and add detail - split each edge at its midpoint, and move the point up or down randomly.
The maximum amount of displacement possible should decrease as the scale decreases.
Sample code: mountain1d.py
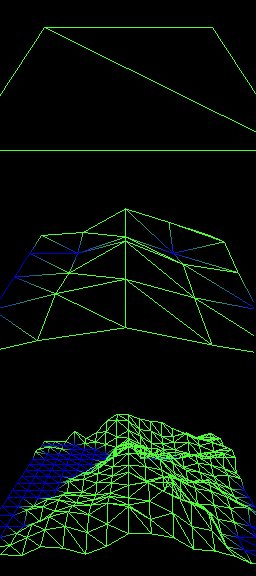
Fractal terrain that is a full 2D surface (rather than 1D line) is created by making a grid of points, and applying the midpoint subdivision approach.
Sample code: mountain2d.py
 A fractal heightfield can also be used for other purposes.
A fractal heightfield can also be used for other purposes.
e.g.: clouds, noise textures
Sample code: heightfield.py