Transformations are functions that take a position and return a new position
newpos = ApplyRotation(oldpos)
All GL transformations (translate, rotate, scale) are simple operations on the (X, Y, Z) values of points
Translation is addition of an offset. e.g. to translate by (-1, 0, 3):
newx = oldx + -1
newy = oldy + 0
newz = oldz + 3
or
[ newx newy newz ] = [ oldx oldy oldz ] + [ -1 0 3 ]
Scaling multiplies each coordinate by a value:
newx = oldx * sx
newy = oldy * sy
newz = oldz * sz
Rotation about the Z axis:
newx = oldx * cos(a) - oldy * sin(a)
newy = oldx * sin(a) + oldy * cos(a)
newz = oldz
Rotation about X or Y is similar, with just the x, y, & z variables shuffled around.
Rotation about an arbitrary axis is more complex, but based on the same idea
In general, the math for any transformation, or combination of transformations, looks like:
newx = A * oldx + B * oldy + C * oldz + D
newy = E * oldx + F * oldy + G * oldz + H
newz = I * oldx + J * oldy + K * oldz + L
This can be simplified by treating positions as 4-coordinate vectors, where the last coordinate (w) is usually 1.
The transformation is then a 4x4 matrix that is the vectors are multiplied by.
| A E I M |
[ X Y Z W ] = [ x y z w ] * | B F J N |
| C G K O |
| D H L P |
In some cases, the matrix transformation is written flipped around:
| x | | A B C D | | x |
| y | = | E F G H | * | y |
| z | | I J K L | | z |
| w | | M N O P | | w |
The two are mathematically the same.
The identity matrix, generated by glLoadIdentity(), leaves vertex data unchanged:
| 1 0 0 0 |
| 0 1 0 0 |
| 0 0 1 0 |
| 0 0 0 1 |
A translation matrix looks like:
| 1 0 0 0 |
| 0 1 0 0 |
| 0 0 1 0 |
| tx ty tz 1 |
e.g. translating by (-1, 0, 3) is
| 1 0 0 0 |
[ x y z 1 ] * | 0 1 0 0 |
| 0 0 1 0 |
| -1 0 3 1 |
The matrices for translation, rotation, scaling, and projections are all described in Appendix F of the OpenGL book.
Two transformations are combined by multiplying their matrices.
e.g. glTranslatef(-1,0,3); glRotatef(45, 0, 0, 1) yields:
| .707 -.707 0 0 | | 1 0 0 0 | | .707 -.707 0 0 | | .707 .707 0 0 | * | 0 1 0 0 | = | .707 .707 0 0 | | 0 0 1 0 | | 0 0 1 0 | | 0 0 1 0 | | 0 0 0 1 | | -1 0 3 1 | | -1 0 3 1 |
The inverse of a transformation T has as its matrix the inverse of T's matrix.
i.e. T * T-1 = Identity
Transformations that do not change the shape or volume of an object - no scaling, shearing, perspective, etc.
Composed of translation and rotation
Representations for rotation:
Represent any arbitrary rotation as rotation-about-X, rotation-about-Y,
rotation-about-Z
Sometimes described as "Heading, Pitch, Roll" or similar
Generally human-friendly
Problems:
Represent any rotation by its 3x3 matrix
Or, represent translation + rotation by 4x4 matrix
Good for combining transformations and other mathematical manipulations
Not so human-friendly
Interpolation can yield non-rigid-body transformations
Similar to axis + angle representation
4-element vector: [ qw qx qy qz ] = qw + qx * i + qy * j + qz * k
i*i = -1, j*j = -1, k*k = -1, i*j = k, j*i = -k, etc.
qw = cos(angle/2)
qx = axisX * sin(angle/2)
qy = axisY * sin(angle/2)
qz = axisZ * sin(angle/2)
Combine quaternions by multiplying them
Interpolate them with "slerp" (spherical linear interpolation) or "nlerp" (normalized linear interpolation)
Grabbing an object, or dynamically attaching one to another, requires manipulating transformations.
Easiest using matrix representation of transformations
If object A has world-relative transformation TA, and object B starts out by itself, then becomes attached to A,
when B is not attached to anything, its world transformation is T1B
when B is attached to A, it will use a transformation T2B,
and its world transformation is T2B * TA
At the moment of attachment, we want these two transformations to be the same.
So, T2B = T1B * TA-1

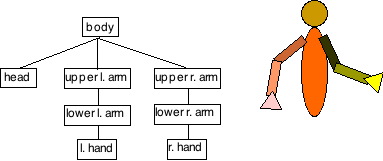
Basic transformations of a character's body parts produce motion like a puppet made of rigid parts.
For a soft-skinned character, one must blend the effects of multiple transformations.
Example: vertexblend.py
