

We often would like the behavior of a program to change or be unpredictable - to not be exactly the same every time we run it.
In other cases, randomness helps eliminate unwanted artifacts, such as obvious, excessively regular or repeated patterns. These include patterns in the appearance and in the movement of objects.
 | 
|
Things that can be randomized include:
Randomness is added to programs by using random numbers. These are generated by random number functions.
Python has a package called random.
Two of the functions it provides are:
Returns a random floating point number between 0 and 1.
Returns a random floating point number between a and b.
In C, the standard random number functions are:
Returns a random integer between 0 and RAND_MAX
Returns a random float between 0 and 1
Random numbers can come in different distributions - how frequently the various numbers occur.
e.g. rolling a fair die many times will yield roughly
the same number of 1s, 2s, 3s, 4s, 5s, and 6s.
A loaded die can produce one number more frequently.
random() & uniform()
return uniform distributions - each possible number is equally
likely to be returned.
If you call the function a large number of times, then you
can expect each possible number to be returned about (but not exactly)
the same number of times.
(Flipping a coin 1,000,000 times, you would expect to get roughly
500,000 heads and 500,000 tails.)
This plot is from calling int(random() * 100) 100,000 times. It shows how many times each of the possible values (from 0 to 99) was returned.
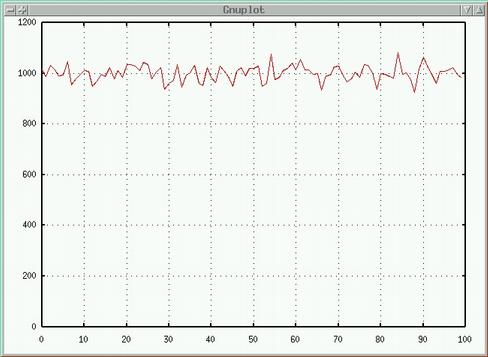
Sometimes we want a different distribution.
A common distribution is the bell curve (or gaussian distribution). In this distribution, one small range of numbers is returned more frequently than others, with values further from the center of the distribution returned less and less frequently.
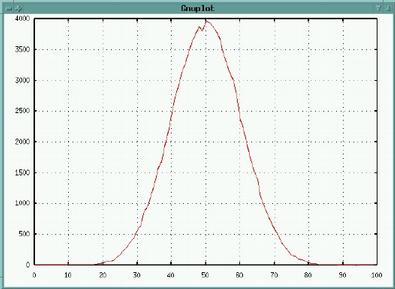
The function random.gauss(center, deviation) returns random numbers in a gaussian distribution.
The first argument (center) is the central number that the return
values will be clustered around. The second argument (deviation)
is the standard deviation of the distribution - this measures how broad the
bell curve is; roughly 2/3 of all returned values will be within +/- deviation
of the center value.
Example: a gaussian distribution lets you place objects randomly, but clustered about a center.
| Uniform | Gaussian |
|---|---|

| 
|
A vector is a direction and magnitude (length). Vectors are used to represent many different things - light source directions, surface orientations, relative distances between objects, etc.
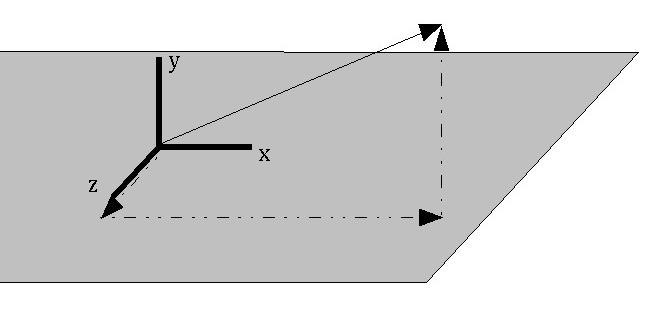
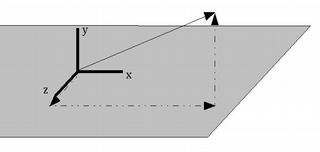
We normally describe a vector as a triplet of (X, Y, Z) values - (vx, vy, vz) represents a vector that points vx units in the direction of the X axis, vy units in the direction of the Y axis, and vz units in the direction of the Z axis.
e.g., (2, 0, 0) is a vector pointing in the direction of the X axis, 2 units long. (1, 1, 0) is a vector pointing at a 45 degree angle between the X and Y axes, 1.414 units long.
The magnitude of a vector (x,y,z) is its Euclidean length - the square root of vx2 + vy2 + vz2.
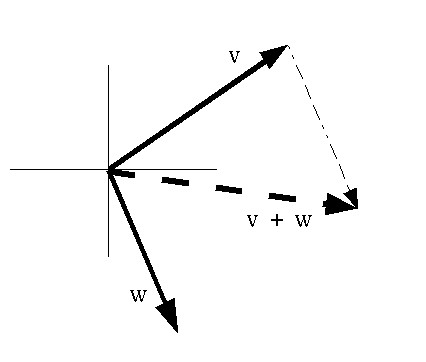
Two vectors can be combined by adding their corresponding components
together.
i.e. (vx, vy, vz) +
(wx, wy, wz) is
(vx+wx, vy+wy, vz+wz
).
Or, written more expansively:
| vx | | wx | | vx + wx | | vy | + | wy | = | vy + wy | | vz | | wz | | vz + wz |
The result is a vector that is equivalent to sticking the vector W onto the end of vector V, and creating a new vector from the beginning of V to the end of W.
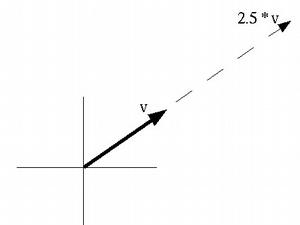
A vector can be multiplied by a single number (a "scalar") to change its length without changing its direction.
| vx | | s * vx |
s * | vy | = | s * vy |
| vz | | s * vz |
The dot product of two vectors is an operation defined as:
| x0 | | x1 | | y0 | * | y1 | = x0*x1 + y0*y1 + z0*z1 | z0 | | z1 |The result is a single number, which is equal to the product of the lengths of the two vectors and the cosine of the angle between them.
It can tell us how much two vectors point in the same direction - it is maximum when they point in exactly the same direction, and it's 0 when they're at right angles.
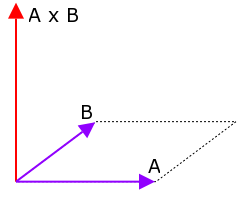
The cross product is a function of two vectors that will produce a new vector perpendicular to both. The length of the cross product is equal to the area of the parallelogram formed by the two vectors.
The formula for the cross product of two vectors A & B is:
[ ( Ay Bz - Az By ), ( Az Bx - Ax Bz ), ( Ax By - Ay Bx ) ]
The Python equivalent is:
def crossProduct(A,B):
return [ A[1] * B[2] - A[2] * B[1],
A[2] * B[0] - A[0] * B[2],
A[0] * B[1] - A[1] * B[0] ]
The direction of the cross product is determined by the right-hand rule applied from vector A to vector B (so if you multiply them in the reverse order, the result will point the opposite direction).
A vector can be used to represent the motion of an object.
The vector indicates the object's velocity - the direction of the vector is the direction that the object is moving, the magnitude of the vector is the speed.
The vector corresponds to how the object will move in one unit of time.
e.g., a velocity vector of (2, 0, 0) indicates that the object is
moving 2 meters/second along the X axis (assuming our units are meters
and seconds).
If it starts at (3, 1, 0), then after 1 second its position will be
(5, 1, 0). After 2 seconds, its position will be (7, 1, 0).
[Note that the choice of units is arbitrary, and is up to you when writing your programs; all that matters is that you be consistent within a program, and not, for instance, try to combine meters per second with miles per hour.]
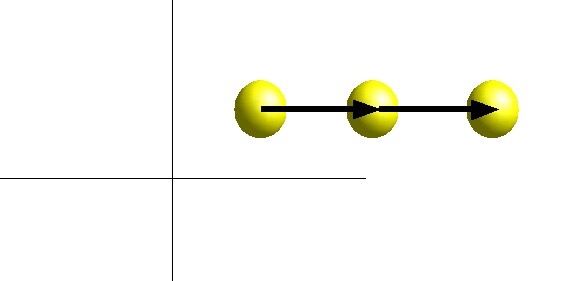
In general, if an object starts at position P0, with velocity V, then after t time units, its position P(t) will be:
P(t) = P0 + t * V
Creating a vector class allows one to work with vectors more simply.
Vector operations just require a single statement, rather than a loop or separate statements for X, Y, & Z components.
a = Vector((1, 2, 3))
b = Vector((0, -1, 0))
c = a + 2 * b
d = a.dot(b)
Misc functions:
