Math

• Distances
• Trigonometry
• Interpolation

Pythagorean Theorem

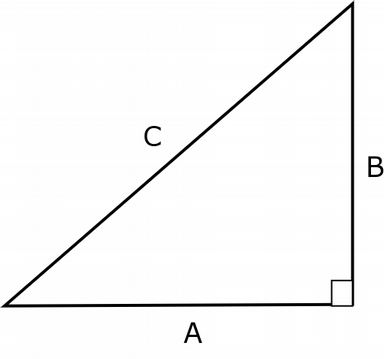
A*A + B*B = C*C

Cartesian Coordinates

Euclidean Distance

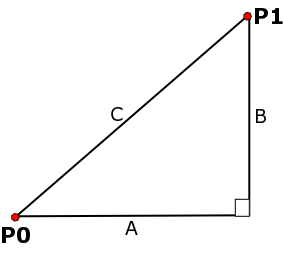
Distance between two points P0 (x0,y0) and P1 (x1,y1):

   A = x1 - x0
   B = y1 - y0

   (x1-x0)*(x1-x0) + (y1-y0)*(y1-y0) = C*C

   dist = C = sqrt((x1-x0)*(x1-x0) + (y1-y0)*(y1-y0))

Distance between two 3D points P0 (x0,y0,z0) and P1 (x1,y1,z1):

   dist = sqrt((x1-x0)*(x1-x0) + (y1-y0)*(y1-y0) + (z1-z0)*(z1-z0))

Comparing Distances

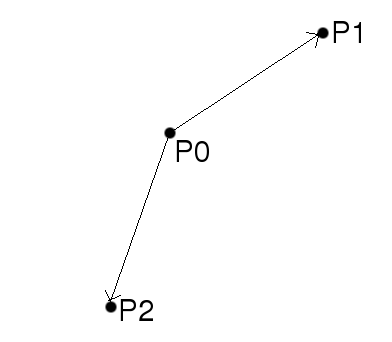
sqrt is considered an expensive (i.e. slow) function

Avoid using it if you can
For example, to determine which of 2 points (P1 or P2) is closer to point P0:

  dist1 = (x1-x0)*(x1-x0) + (y1-y0)*(y1-y0) + (z1-z0)*(z1-z0)
  dist2 = (x2-x0)*(x2-x0) + (y2-y0)*(y2-y0) + (z2-z0)*(z2-z0)
  if dist1 < dist2:
        P1 is closer
  else:
        P2 is closer

Trigonometry

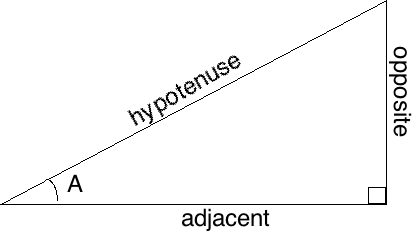
sin(A) = opposite / hypotenuse
cos(A) = adjacent / hypotenuse
tan(A) = opposite / adjacent

or

opposite = hypotenuse * sin(A)
adjacent = hypotenuse * cos(a)

Trigonometry

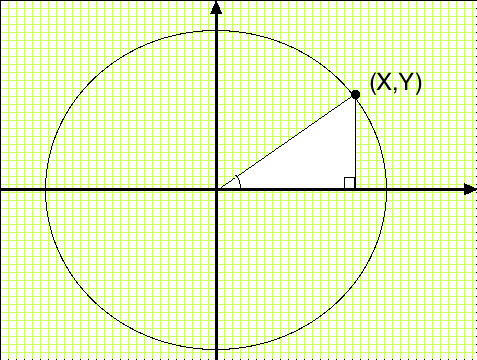
x = radius * cos(A)
y = radius * sin(A)

Radians

Standard math library functions use radians

360 degrees = 1 full circle = 2 π radians

(Circumference of unit circle = 2 π)

    radians = degrees / 360.0 * 2 * pi

or

    radians = degrees / 180.0 * pi

Making a Circle

    vertices = []
    for degrees in range(0, 360): 
        angleInRadians = math.radians(degrees)
        x = math.cos(angleInRadians) * radius
        y = math.sin(angleInRadians) * radius
        vertices += [x,y]
    vlist = pyglet.graphics.vertex_list(360, ('v2f', vertices))

Driving

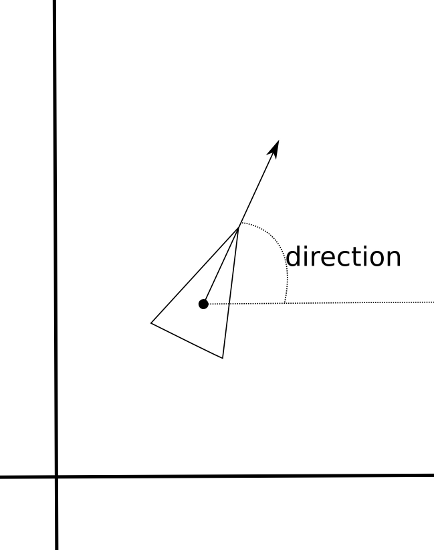
Vehicle has direction and speed of travel

Direction is orientation - rotation about Z

To move forward:

    distance = speed * time

    dx = math.cos(direction) * distance
    dy = math.sin(direction) * distance

    x = x + dx
    y = y + dy

atan2

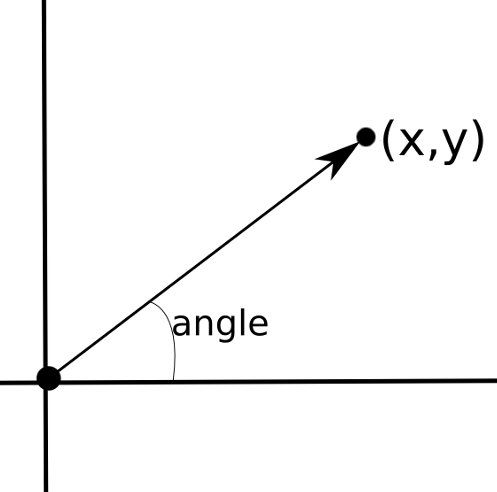
atan2 converts from (X,Y) coordinates back to angles

Note: it takes arguments in the order Y, X

 
    angle = math.degrees( math.atan2(y,x) )

Interpolation

Deriving a value for something from two pre-defined values (extremes)

e.g. Moving object from one position to another, over time

Linear Interpolation

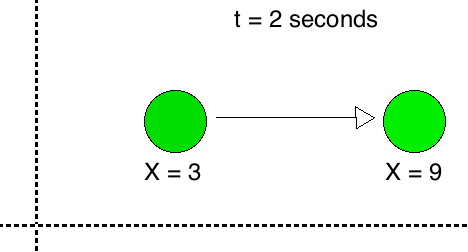
Interpolation expressed as fractional distance between the two extremes

Ranges from 0.0 to 1.0
0.0 = first point; 1.0 = second point

Linear Interpolation

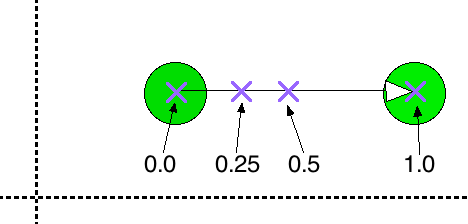
For a single value, with extremes V0 & V1 and interpolation fraction A:

    V = (1 - A) * V0 + A * V1

For multiple values, such as XYZ position, use the same fraction A for all:

    X = (1 - A) * X0 + A * X1
    Y = (1 - A) * Y0 + A * Y1
    Z = (1 - A) * Z0 + A * Z1

Timing

To interpolate over time, compute interpolation fraction based on the amount of time that has passed.

Example:

    def startAnimation():
        animating = True
        startTime = time.time()
        duration = 5

    def computeAnimation():
        if animating:
            t = time.time() - startTime
            if t <= duration:
                a = t / duration
            else:
                animating = False
                a = 1
            x = (1-a)*startX + a*endX
            y = (1-a)*startY + a*endY
            z = (1-a)*startZ + a*endZ

Timing

Linear	Slow-in Slow-out
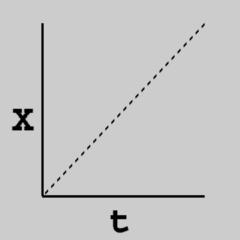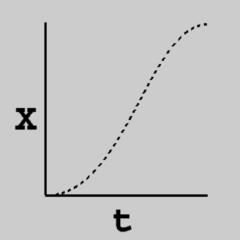X = t	X = -2*t*t*t + 3*t*t

A2 = -2*A*A*A + 3*A*A
V = (1-A2) * V0 + A2 * V1

This document is by Dave Pape, and is released under a Creative Commons License.